Click-Through Rate Prediction
Dmitry Efimov
AUS-ICMS'15
April, 5, 2015
Outline
Provided data
Likelihood features
FTRL-Proximal Batch algorithm
Factorization Machine algorithm
Competition
Provided data
Notations
$\boldsymbol{X}$: $\boldsymbol{m \times n}$ design matrix |
$
\Tiny
\begin{array}{l}
\quad\\
\quad \boldsymbol{m}_{\mbox{train}} \boldsymbol{= 40\,428\,967}\\
\quad \boldsymbol{m}_{\mbox{test}} = \boldsymbol{4\,577\,464}\\
\quad \boldsymbol{n = 23}\\
\quad
\end{array}
$
|
$\boldsymbol{y}$: binary target vector of size $m$ |
$\boldsymbol{x^j}$: column $\boldsymbol{j}$ of matrix $\boldsymbol{X}$ |
$\boldsymbol{x_i}$: row $\boldsymbol{i}$ of matrix $\boldsymbol{X}$ |
$\boldsymbol{\sigma(z) = \dfrac{1}{1 + e^{-z}}}$: sigmoid function |
Evaluation
Logarithmic loss for \(y_i \in \{0, 1\}\): \[ \boldsymbol{L = -\dfrac{1}{m} \sum\limits_{i=1}^{m} \left(y_i \log (\hat{y}_i) + (1-y_i) \log(1-\hat{y}_i)\right)} \] \(\Tiny \boldsymbol{\hat{y}_i} \mathbf{\mbox{ is a prediction for the sample }} \boldsymbol{i}\)
Logarithmic loss for \(y_i \in \{-1, 1\}\):
\[
\boldsymbol{L = \dfrac{1}{m} \sum\limits_{i=1}^{m} \log (1 + e^{-y_i p_i})}
\]
\(\Tiny \boldsymbol{p_i} \mathbf{\mbox{ is a raw score from the model}}\)
\(\Tiny \boldsymbol{\hat{y}_i = \sigma (p_i), \forall i \in \{1, \ldots , m\}}\)
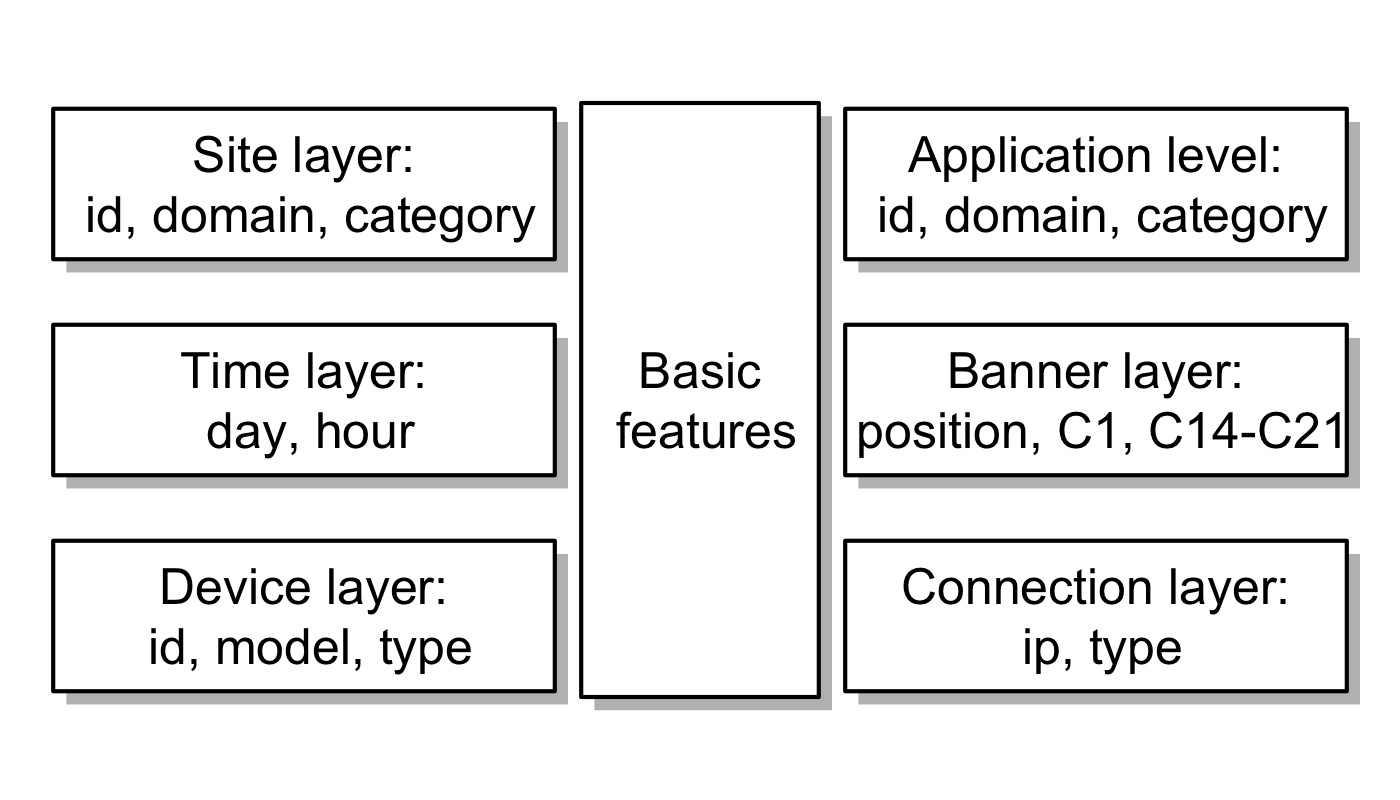
Feature engineering
- Blocks: combination of two or more features
- Counts: number of samples for different feature values
- Counts unique: number of different values of one feature for fixed value of another feature
- Likelihoods: \(\;\min\limits_{\theta_t} L,\;\) where \(\;\theta_{t} = P(y_i\;|\;x_{ij} = t)\)
- Others
Feature engineering (algorithm 1)
|
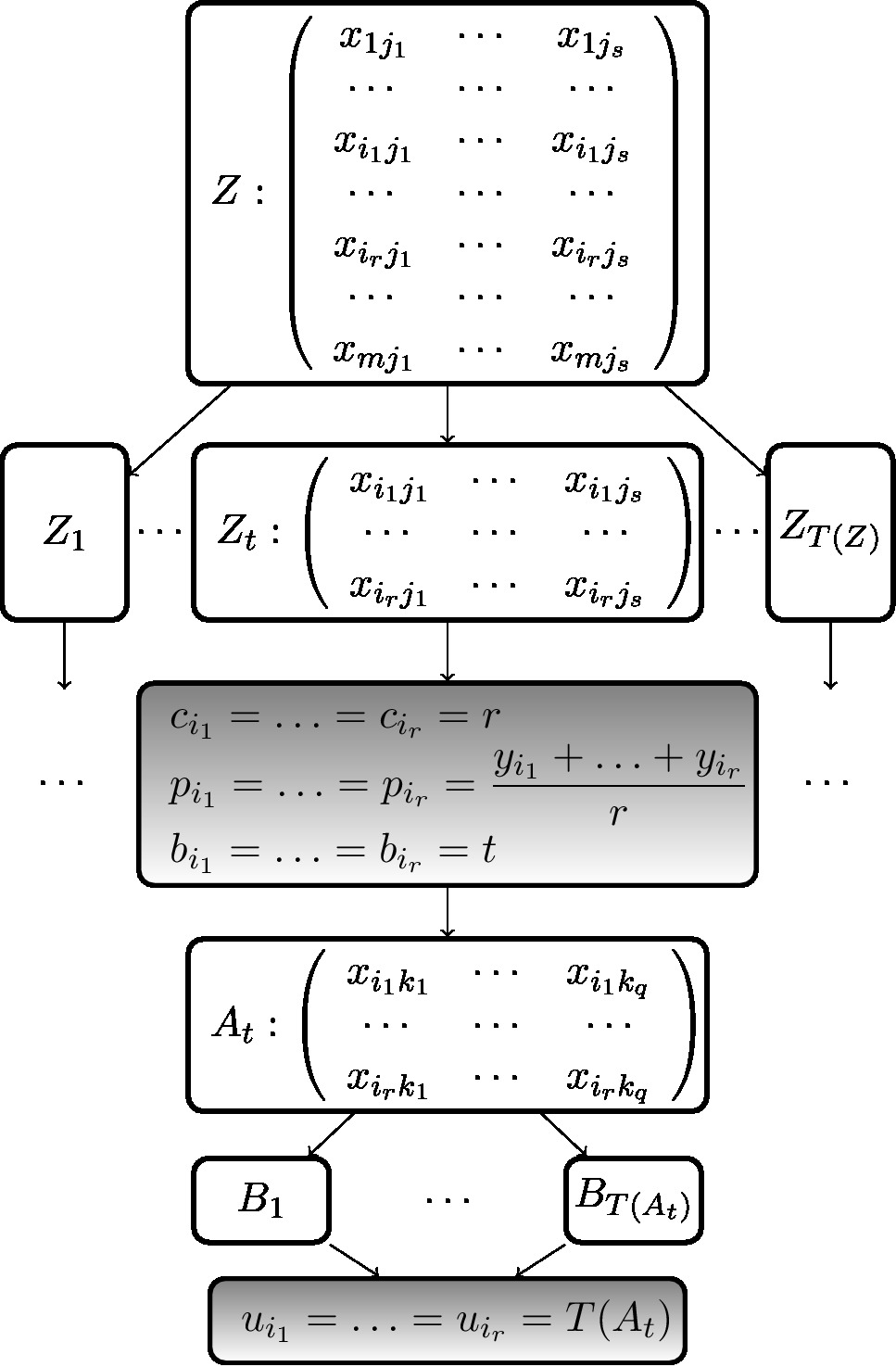
$$ \tiny \begin{array}{l} \mathbf{\mbox{function }} \mbox{splitMatrixByRows}(\boldsymbol{M})\\ \quad\mbox{get partition of the matrix }\boldsymbol{M}\mbox{ into }\boldsymbol{\{M_t\}}\\ \quad\mbox{by rows such that each }\boldsymbol{M_t}\mbox{ has identical rows}\\ \mathbf{\mbox{require:}}\\ \quad \boldsymbol{J \gets \{j_1, \ldots , j_s \} \subset \{1, \ldots , n\}}\\ \quad \boldsymbol{K \gets \{k_1, \ldots , k_q\} \subset \{1, \ldots , n\} \setminus J}\\ \quad \boldsymbol{Z \gets ( x_{ij} ) \subset X, i \in \{1, 2, \ldots, m\}, j \in J}\\ \mathbf{\mbox{for }} \boldsymbol{I = \{i_1, \ldots , i_r\} \in} \mbox{splitMatrixByRows}(\boldsymbol{Z})\\ \quad \boldsymbol{c_{i_1} = \ldots = c_{i_r} = r}\\ \quad \boldsymbol{p_{i_1} = \ldots = p_{i_r} = \dfrac{y_{i_1} + \ldots + y_{i_r}}{r}}\\ \quad \boldsymbol{b_{i_1} = \ldots = b_{i_r} = t}\\ \quad \boldsymbol{A_t = (x_{ik}) \subset X, i \in I, k \in K}\\ \quad \boldsymbol{u_{i_1} = \ldots = u_{i_r} = }\mbox{size}(\mbox{splitMatrixByRows}(\boldsymbol{A_t}))\\ \end{array} $$ |
Feature engineering (algorithm 2)
\[ \tiny \begin{array}{l} \mathbf{\mbox{require:}}\\ \quad \mbox{parameter } \boldsymbol{\alpha}\\ \quad \boldsymbol{J \gets \{j_1, \ldots , j_s \} \subset \{1, \ldots , n\}}\\ \quad \mbox{increasing sequence of jumps } \boldsymbol{V \gets (v_1, \ldots v_l) \subset \{1, \ldots , s\}, v_1 < s}\\ \quad \boldsymbol{f_i \gets \dfrac{y_1 + \ldots + y_m}{m}, \forall i \in \{1, \ldots , m\}}\\ \mathbf{\mbox{for }} \boldsymbol{v \in V}\\ \quad \boldsymbol{J_v = \{j_1, \ldots , j_v\}, Z = ( x_{ij} ) \subset X, i \in \{1, 2, \ldots, m\}, j \in J_v}\\ \quad \mathbf{\mbox{for }} \boldsymbol{I = \{i_1, \ldots , i_r\} \in} \mbox{splitMatrixByRows}(\boldsymbol{Z})\\ \quad\quad \boldsymbol{c_{i_1} = \ldots = c_{i_r} = r}\\ \quad\quad \boldsymbol{p_{i_1} = \ldots = p_{i_r} = \dfrac{y_{i_1} + \ldots + y_{i_r}}{r}}\\ \quad \boldsymbol{w = \sigma(-c + \alpha)} \mbox{ - weight vector}\\ \quad \boldsymbol{f_i = (1 - w_i) \cdot f_i + w_i \cdot p_i, \forall i \in \{1, \ldots , m\}}\\ \end{array} \]
FTRL-Proximal model
\[ \Tiny \begin{array}{l} \mbox{Weight updates:}\\ \boldsymbol{w_{i+1} = \arg \min\limits_{w} \left( \sum\limits_{r = 1}^{i} g_r \cdot w + \dfrac{1}{2}\sum\limits_{r=1}^{i} \tau_r ||w - w_{r}||^2_2 + \lambda_1 ||w||_1\right) =}\\ \boldsymbol{= \arg \min\limits_{w} \left( w \cdot \sum\limits_{r = 1}^{i} (g_r - \tau_r w_r) + \dfrac{1}{2} ||w||_2^2 \sum\limits_{r=1}^{i} \tau_r + \lambda_1 ||w||_1 + \mbox{const}\right),}\\ \mbox{where } \boldsymbol{\sum\limits_{r=1}^{i} \tau_{rj} = \dfrac{\beta + \sqrt{\sum\limits_{r=1}^{i} \left(g_{rj}\right)^2}}{\alpha} + \lambda_2 , \; j \in \{1, \ldots , N\},}\\ \boldsymbol{\lambda_1, \lambda_2, \alpha, \beta} \mbox{ - parameters}, \boldsymbol{\tau_r = (\tau_{r1}, \ldots , \tau_{rN})} \mbox{ - learning rates},\\ \boldsymbol{g_r} \mbox{ - gradient vector for the step } \boldsymbol{r} \end{array} \]
FTRL-Proximal Batch model
\[ \tiny \begin{array}{l} \mathbf{\mbox{require:}} \mbox{ parameters }\boldsymbol{\alpha, \beta, \lambda_1, \lambda_2}; \mathbf{\mbox{initialize: }} \boldsymbol{z_j \gets 0, n_j \gets 0, \forall j \in \{1, \ldots , N\}}\\ \mathbf{\mbox{for }} \boldsymbol{i = 1} \mbox{ to } \boldsymbol{m}\\ \quad \mbox{receive sample vector }\boldsymbol{x_i}\mbox{ and let }\boldsymbol{J = \{\,j\;|\;x_{ij} \neq 0\,\}}\\ \quad \mathbf{\mbox{for }} \boldsymbol{j \in J}\\ \quad\quad \boldsymbol{w_{j} = }\left\{\begin{array}{ll} \boldsymbol{0} & \mbox{if } \boldsymbol{| z_j | \leqslant \lambda_1} \\ \boldsymbol{-\left(\dfrac{\beta + \sqrt{\vphantom{\sum}n_j}}{\alpha} + \lambda_2\right)^{-1} \left(z_j - sign(z_j) \lambda_1 \right)} & \mbox{otherwise}\end{array}\right.\\ \quad \mbox{predict }\boldsymbol{\hat{y}_i = \sigma(x_i \cdot w)} \mbox{ using the }\boldsymbol{w_j}\mbox{ and observe label }\boldsymbol{y_i}\\ \quad \mathbf{\mbox{if }} \boldsymbol{y_i \in \{0, 1\}}\\ \quad\quad \mathbf{\mbox{for }} \boldsymbol{j \in J}\\ \Tiny \quad\quad\quad \begin{array}{ll}\boldsymbol{g_j = \hat{y}_i - y_i} & \boldsymbol{\tau_j = \frac{1}{\alpha} \left(\sqrt{n_j + {g_j}^2} - \sqrt{\vphantom{\sum}n_j}\right)}\\ \boldsymbol{z_j \leftarrow z_j + g_j - \tau_j w_j} & \boldsymbol{n_j \leftarrow n_j + {g_j}^2} \end{array}\\ \end{array} \]
Performance
| Description |
Leaderboard score |
|---|---|
|
dataset is sorted by app id, site id, banner pos, count1, day, hour |
0.3844277 |
|
dataset is sorted by app domain, site domain, count1, day, hour |
0.3835289 |
| dataset is sorted by person, day, hour | 0.3844345 |
|
dataset is sorted by day, hour with 1 iteration |
0.3871982 |
|
dataset is sorted by day, hour with 2 iterations |
0.3880423 |
Factorization Machine (FM)
Second-order polynomial regression:
\[
\hat{y} = \sigma\left(\sum\limits_{j = 1}^{n-1} \sum\limits_{k = j+1}^{n} w_{jk} x^j x^k\right)
\]
Low rank approximation (FM):
\[ \hat{y} = \sigma\left(\sum\limits_{j = 1}^{n-1} \sum\limits_{k = j+1}^{n} (v_{j1}, \ldots , v_{jH}) \cdot (v_{k1}, \ldots , v_{kH}) x^j x^k\right) \]
\(H\) is a number of latent factors
Factorization Machine for categorical dataset
Assign set of latent factors
for each pair level-feature:
\[
\Tiny
\boldsymbol{\hat{y}_i = \sigma\left(\dfrac{2}{n} \sum\limits_{j = 1}^{n-1} \sum\limits_{k = j+1}^{n} (w_{x_{ij}k1}, \ldots , w_{x_{ij}kH}) \cdot (w_{x_{ik}j1}, \ldots , w_{x_{ik}jH})\right)}
\]
Add regularization term: \(\Tiny \boldsymbol{L_{reg} = L + \dfrac{1}{2} \lambda ||w||^2}\)
The gradient direction: \[ \Tiny \boldsymbol{g_{x_{ij} k h} = \dfrac{\partial L_{reg}}{\partial w_{x_{ij} k h}} = -\dfrac{2}{n} \cdot \dfrac{y_i e^{-y_i p_i}}{1 + e^{-y_i p_i}} \cdot w_{x_{ik}jh} + \lambda w_{x_{ij}kh}} \]
Learning rate schedule: \(\Tiny \boldsymbol{\tau_{x_{ij}kh} = \tau_{x_{ij}kh} + \left(g_{x_{ij} k h}\right)^2}\)
Weight update: \(\Tiny \boldsymbol{w_{x_{ij}kh} = w_{x_{ij}kh} - \alpha \cdot \sqrt{\vphantom{\sum}\tau_{x_{ij}kh}} \cdot g_{x_{ij} k h}}\)
Ensembling
| Model name | Description |
Leaderboard score |
|---|---|---|
| ftrlb1 | dataset is sorted by app id, site id, banner pos, count1, day, hour | 0.3844277 |
| ftrlb2 | dataset is sorted by app domain, site domain, count1, day, hour | 0.3835289 |
| ftrlb3 | dataset is sorted by person, day, hour | 0.3844345 |
| fm | factorization machine | 0.3818004 |
| ens | $\Tiny \boldsymbol{\mbox{fm}^{0.6} \cdot \mbox{ftrlb1}^{0.1} \cdot \mbox{ftrlb2}^{0.2} \cdot \mbox{ftrlb3}^{0.1}}$ | 0.3810447 |
Final results
| Place | Team |
Leaderboard score |
Difference between the 1st place |
|---|---|---|---|
| 1 | 4 idiots | 0.3791384 | --- |
| 2 | Owen | 0.3803652 | 0.32% |
| 3 | Random Walker | 0.3806351 | 0.40% |
| 4 | Julian de Wit | 0.3810307 | 0.50% |
| 5 | Dmitry Efimov | 0.3810447 | 0.50% |
| 6 | Marios and Abhishek | 0.3828641 | 0.98% |
| 7 | Jose A. Guerrero | 0.3829448 | 1.00% |
Future work
- apply batching idea to the Factorization Machine algorithm
- find better sorting for the FTRL-Proximal Batch algorithm
- find an algorithm that can find better sorting without cross-validation procedure
References
H.Brendan McMahan et al. Ad click prediction: a view from the trenches. In KDD, Chicago, Illinois, USA, August 2013
Wei-Sheng Chin et al. A learning-rate schedule for stochastic gradient methods to matrix factorization. In PAKDD, 2015
Michael Jahrer et al. Ensemble of collaborative filtering and feature engineered models for click through rate prediction. In KDD Cup, 2012
Steffen Rendle. Social network and click-through prediction with factorization machines. In KDD Cup, 2012
Thank you!
Dmitry Efimov
defimov@aus.edu
Questions?
